Редакция сердечно благодарит автора

за разрешение опубликовать без вознаграждения этот рисунок.

Женское наблюдение:

"Жизнь полна невзгод и страданий. Горя и ненависти. Разочарований и предательства. А потом, наконец, вы находите именно того парикмахера, который вам нужен!.."

Вступительное тестирование

8 мая 2005 года в 21 школе состоится очередное вступительное тестирование. Начало тестирования для учеников 8-12 классов в 10:00, а для учеников 6-7 классов -- в 12:00. С собой следует иметь ученический билет, ручку и 70 сантимов ученикам 8-12 классов и 40 сантимов ученикам 6-7 классов. Поступающий должен знать свой персональный код. Чтобы быть допущенным к тестированию, следует до 6 мая зарегистрироваться по адресу www.progmeistars.lv или по телефону 7336035.

По результатам тестирования будут пополняться начальное и основное отделения. Весной на начальное отделение принимаются школьники шестого и седьмого классов.

На основное отделение весной принимаются школьники, начиная с восьмого класса, и учащиеся средних специальных учебных заведений. Если поступивший умеет программировать на Pascal'е, то он может заявить об этом при регистрации, и, после собеседования, его могут принять сразу на второй семестр.

Наших выпускников ждут!

Мы уже один раз писали об успешном трудоустройстве наших выпускников. Поскольку предложения от фирм продолжают поступать, то редакция повторяет заметку из КурсоWeek’a #37.

Уважаемые выпускники курсов “Progmeistars” (ранее “Fortek”)! Сейчас на рынке труда нарастает спрос на программистов. Работодатели, предлагая достойную заработную плату, предъявляют серьезные требования к квалификации своих сотрудников. Как вы знаете, на курсах Progmeistars, еще будучи школьниками, вы серьезно изучаете общие методы программирования, методы построения и анализа алгоритмов. Наше кредо: учить так, чтобы потом вам не было мучительно трудно, а нам - мучительно стыдно. Поэтому работодатели сообщают нам о вакансиях на своих фирмах, с тем, чтобы к ним на работу пришли вы - наши выпускники. Рекомендации Progmeistars’a высоко котируются. (Кстати, по нашим рекомендациям делают скидку за обучение в Интитуте транспорта и связи TSI).

Пишите (direktors@progmeistars.lv) и/или звоните (7336035)

"Ugāle 2005".

С 1996 года в Угале под руководствсвом замечательного преподавателя Айвара Жоглы проводятся командные соревнования по информатике и математике KSIM.

По положению каждая команда из трех участников получает задания по программированию, математике и компьютерной обработке данных. В полуфинале KSIM “Ugāle 2005” соревновались 90 команд со всей Латвии. В финале, который состоится 15-го мая, первые 9 из приведенной ниже таблицы будут участвовать обязательно. Согласно положению соревнований, к ним примкнут хозяева и несколько приглашенных команд

Vieta	Skola	Komanda
1	Rīgas Zolitūdes ģimnāzija		1
2	Progmeistars		MRZ
3	Progmeistars		CMW
4	Rīgas Zolitūdes ģimnāzija		3
5	Daugavpils krievu licejs		1
6	Rīgas 40.vidusskola		1
7	Rīgas 40.vidusskola		2
8	Rīgas Valsts 1.ģimnāzija		2
9	Rīgas Valsts 1.ģimnāzija		15
10	Progmeistars		KSK
33	Progmeistars		PMW

От Progmeistars’а стартовали 4 команды. Как видно из таблицы, результаты отличные. Даже 33-ее место – это хорошо, поскольку в команде PMW (Константин Попов, Денис Михайлов, Андрей Вихров) ребята учатся еще только в 9-10 классах. Состав команды MRZ: Михаил Милехин, Андрей Рапопорт, Александр Завальный. Состав команды CMW: Илмарс Цирулис, Владимир Муревич, Мадарс Вирза. Состав команды KSK: Антон Кенга, Игорь Степанов, Иван Киселев.

Отметим, что наши курсанты были и во многих других командах. Пожелаем всем участникам финала в интересной борьбе выступить в полную силу!

Математический гений –

Рамануджан Сриниваза Айенгар

(Ramanujan Srinivasa Aaiyangar 1887-1920)

По материалам сайта «Математика on-line»

http://mathem.h1.ru/ramanudjan.html

Рамануджан родился 22 декабря 1887 г. в селении Эрод, на юге Индии. Его родители принадлежали к привилегированной касте браминов, но жили бедно и ничем не отличались от окружавших их мелких служащих, торговцев и крестьян. Отец Рамануджана был бухгалтером в маленькой текстильной лавке в городе Кумбаконаме Танджорского района Мадрасской провинции.

Когда ему шел пятый год, Рамануджан, как и все мальчики-брамины, был отдан в двухлетнюю школу, по окончании которой он поступил в начальную школу при городской средней школе Кумбаконама, где протекала вся его дальнейшая школьная жизнь. В 1897 г. он окончил начальную школу и занял первое место по результатам стипендиальных экзаменов в районном центре Танджоре, что дало ему право дальнейшего обучения в средней школе за половинную плату.Уже в четвёртом классе средней школы Рамануджан самостоятельно изучил полный курс тригонометрии по двухтомному руководству Лони (Loney). Только в 1903 г., когда Рамануджан был в шестом классе средней школы, ему удалось получить единственную книгу по высшей математике, имевшуюся в Кумбаконаме. Это была книга Карра "Сборник элементарных результатов чистой и прикладной математики", изданная в двух томах в Лондоне в 1880-1886 гг. Книга Карра содержит 6165 теорем и формул, большинство которых приводится без доказательств и выводов; конспективные доказательства намечены только для небольшого числа важнейших теорем.

Шестой класс был последним классом средней школы. В 16 лет Рамануджан по окончании школы выдержал приёмные испытания в Мадрасский университет и в январе 1904 г. приступил к занятиям на первом курсе Кумбаконамского колледжа, входившего в состав Мадрасского университета. За свои первые успехи он получил специальную стипендию, предназначавшуюся для особо успевающих по английскому языку и математике. Однако вскоре его учебные дела в колледже пошли всё хуже и хуже, так как он отдавал всё время собственным математическим исследованиям.

Он перестал выполнять задания, пропускал много занятий и в конце концов был оставлен на первом курсе. В жизни Рамануджана началась полоса неудач, длившаяся почти 10 лет.

До 1909 г. он не имел определённых занятий, если не считать того, что всё это время Рамануджан неустанно занимался математикой, исписывая всё новые и новые страницы своих записных книжек. В 1909 г. Рамануджан женился и начал поиски работы.

К началу 1913 г. близкие к Рамануджану индийские математики настойчиво рекомендовали ему вынести свои результаты из записных книжек на более компетентный и строгий суд: послать их в центр математической мысли Британской империи - Кембриджский университет. Получивший эти письма профессор Кембриджского университета, выдающийся математик Г.Г.Харди, понял, что имеет дело с незаурядным явлением. 17 марта 1914 года Рамануджан отбыл в Англию. Первые месяцы пребывания Рамануджана в Кембридже были посвящены восполнению основных пробелов в его математических знаниях. Профессоры Кембриджского университета Годфри Харольд Харди (1877-1947) и Джон Иденсор Литлвуд (род. в 1885 г.) и другие кембриджские математики были изумлены как глубиной его знаний в одних вопросах, так и его полной неосведомлённостью в других.

Рамануджан упорно занимался математикой и только одной математикой. Он не проявлял ни малейшего интереса ни к каким другим областям, кроме как к анализу и теории чисел. Харди писал: " Его понимание сущности математического доказательства было более чем туманным; он пришёл ко всем своим результатам, как ранним, так и более поздним, как верным, так и неверным, при помощи странной смеси интуитивных догадок, индуктивных соображений и логических рассуждений...". Основная часть опубликованных работ Рамануджана была написана им в Кембридже самостоятельно или в соавторстве с Харди.

Весной 1917 г. Рамануджан заболел и должен был лечь в Кембриджский госпиталь, где его регулярно посещали Харди и другие кембриджские математики. Он имел от рождения слабые лёгкие, и его болезнь перешла в открытую форму туберкулёза. Рамануджану очень хотелось вернуться домой, в Индию, но отъезд задерживался в течение двух лет в связи с его болезненным состоянием и трудностями морского сообщения (воздушного сообщения, конечно, ещё не существовало

26 ноября 1918 г. он был избран в члены Английского Королевского общества. После перееззда в Индию Рамануджан провёл три месяца в Мадрасе, а затем отправился отдыхать в деревню. Силы его быстро угасали, но он не хотел лечиться и лихорадочно работал над своим последним детищем - симулирующими тета-функциями. 26 апреля 1920 г. Рамануджан умер в Чэтпуте - одном из предместий Мадраса.

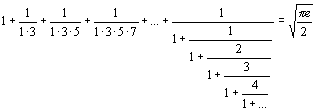
Это, возможно, самая красивая формула Рамануджана. Она неожиданно связыавает бесконечный ряд и бесконечную цепную дробь. Удивительно, что ни ряд, ни цепная дробь не выражаются через известные постоянные p и e, а их сумма непостижимым образом оказывается равной .